エリオット波動8つの特徴⑥実は簡単!比例関係の活用方法

前回の記事では、エリオット波動の出来高について説明した。今回は、エリオット波動の特徴の6つ目、「比率関係」について解説していく。比率関係の計算の仕方、活用方法、様々な比率関係のケースについて伝えていく。
この記事を読むと、目標価格の算出の仕方がわかるので、リターンとリスクを考えたシナリオが立てやすくなる。
・波動の延長
・波動の均等性
・オルタネーション
・チャネリング
・出来高
・比率関係 ←今回はこの話をします
・修正波の深さ
・波動の個性
シナリオというのは今後どのような値動きをするのか?をイメージすることである。
初心者はイメージって言葉を聞くと、予想することや相場の行方を当てることと勘違いをするがシナリオはあくまでも、考えられる可能性の一つでしかない。
しかし、なにか指針を立てて仮説を立てないと話が先に進まないので想定される可能性の中からどれか一つを選ぶ必要がある。その選んだ可能性に基づいてトレード計画を立てる行為を「シナリオを立てる」という。
目次
1. エリオット波動の比率関係
エリオット波動分析では、フィボナッチ数列と呼ばれる自然界の多くで当てはまる数学的な理論を用いて各波動の比率関係を分析できる。具体的に、フィボナッチ数列とは数字同士の比率を並べたもので隣り合う数字同士がフィボナッチ数列の黄金比に近づくと言われている。
わかりやすく説明するとこんな感じ。
例1:隣り合う数を足すと次の数字になる。
2,3,5,8,13,21….
上の数列を左から足し算してみると、
2+3=5、3+5=8、5+8=13、8+13=21となる。
例2:隣り合う数の比率が限りなく黄金比に近づく(自然界の事象で多く見受けられる)。
5,8,13,21,34….
の数列で、大きい数字を小さい数字で割ってみる。
8÷5=1.6、13÷8=1.625、21÷13=1.615、34÷21=1.619となる。
このように完璧な比率数字が出るわけではないが、一般的には小さい数字を大きい数字で割り算した「0.618」と、大きい数字を小さい数字で割り算した「1.618」の2つが使用されている。
また、フィボナッチ数列は離れた数列同士を計算することで他の比率を割り出すことができる。エリオット波動分析で多用するフィボナッチ比率について、図を用いてまとめた。

主要なフィボナッチ比率は、多くのトレーダーが注目している比率でもある。では実際に、フィボナッチ数列がトレードで役に立つのだろうか?
2. 比率関係でわかること

断っておくが、フィボナッチ比率の数字でピタっと止まって反発するといったことはあまりない。よって、確実にここで止まるラインだから買ってみようといった感覚で使うと、良くない思い込みにつながりトレードに悪影響が出る。
では、何のためにこれを知っておく必要があるのか?というと
・波動終点のメドを考察するのに、おおよその見当を付けやすくなる
・波動全体のバランスをチェックしやすい
事実、波動をカウントする際、「本当にインパルスなのか?」「これはダイアゴナルの波形なのか?」と、迷うことがある。そんなとき、フィボナッチ数列の黄金比を用いて波形の種類を推測しやすくする。ただ、あくまでも目安であり、これを覚えたら価格の行末がわかると勘違いしないようにしてほしい。
3. ケース別のエリオット波動の比率関係
エリオット波動の比率関係には、インパルスで延長(エクステンション)した場合、延長がない場合、修正波の比率関係など様々なケースがある。ここでは、それぞれのケースにおける比率関係について説明していく。
これは、別の記事で述べている「波動の延長」「波動の均等性」などとも密接に関係してくるので、そちらの記事も併せて読むことで理解が深まる。
3-1. インパルスのアクション波(1波、3波、5波)同士における比率関係
インパルスで1波、3波、5波のどれかが延長(エクステンション)した場合の比率関係について考察してみよう。
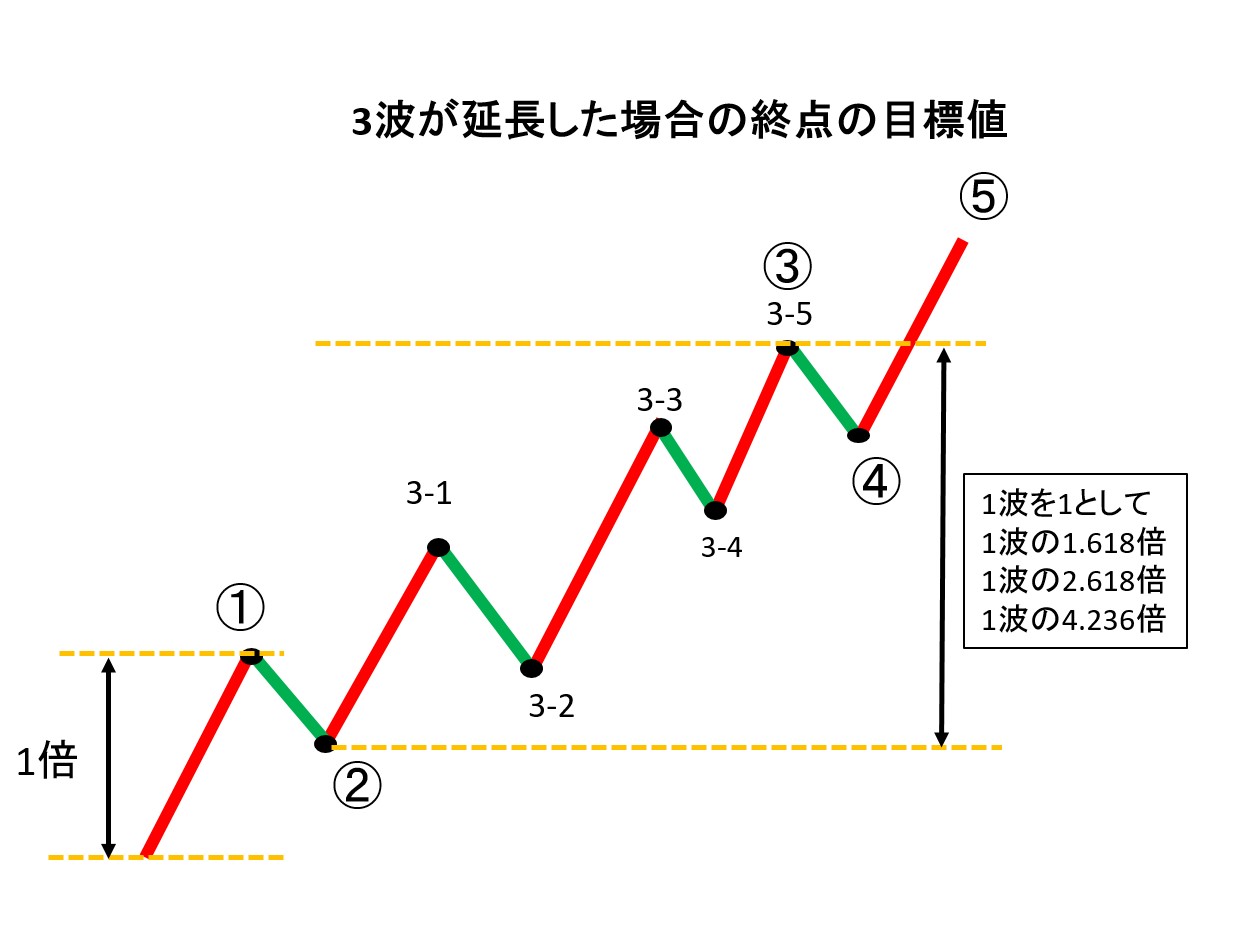
インパルスの1波、3波、5波の中でも、頻度高く延長するのは3波となる。そして、3波の大きさが当てはまるフィボナッチ比率は以下となる。
・1波に対して、1.618倍か2.618倍か4.236倍のどれかが3波終点の目安となる。下図参照
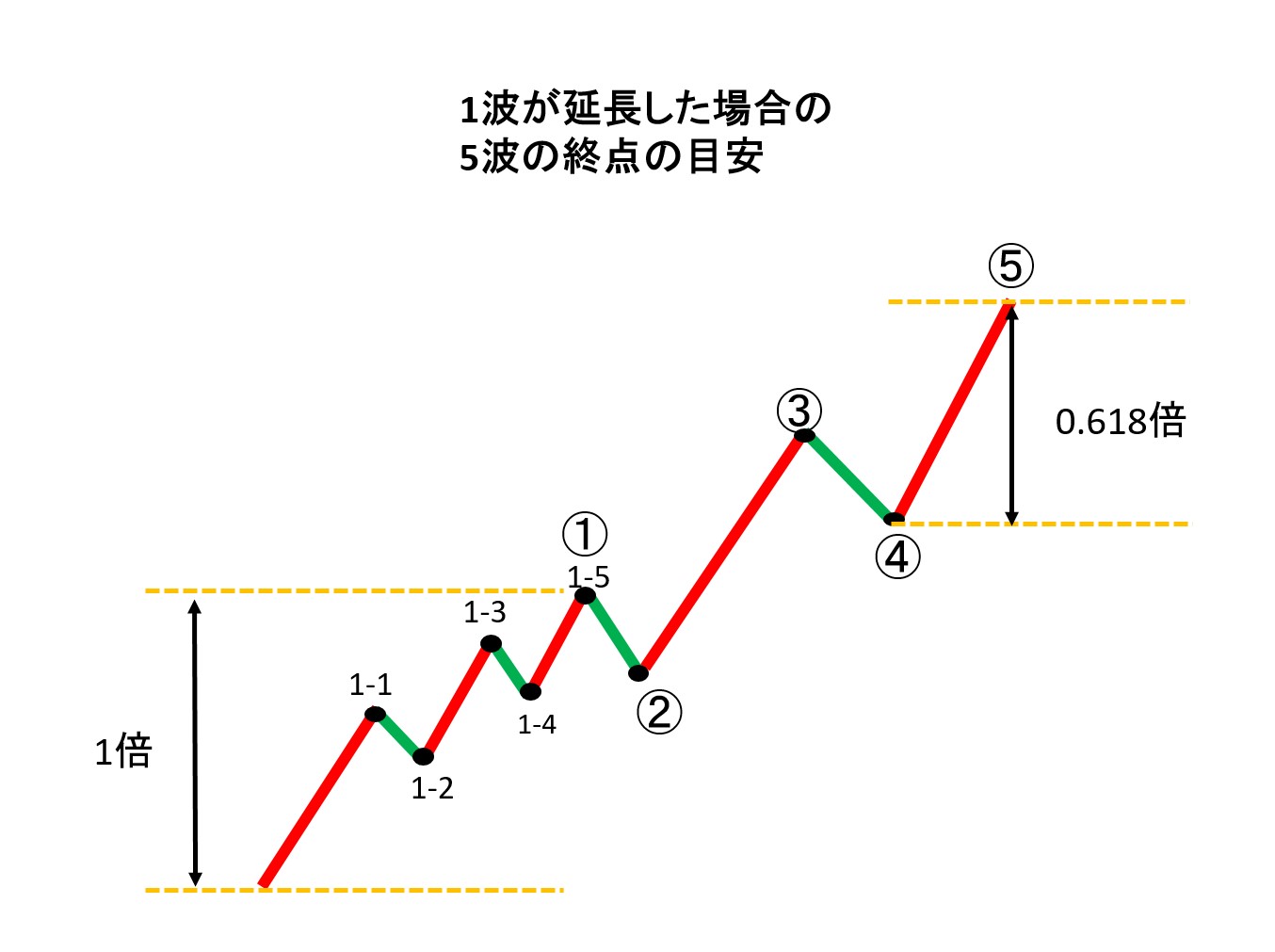
3波以外の、1波と5波の延長(エクステンション)における比率関係についても説明しておく。1波が延長する場合は、2波終点から5波終点までが1波に対して0.618倍となる。下図参照
5波が延長する場合は、1波から3波終点までを比率「1」として5波の大きさは1.618倍となる。下図参照
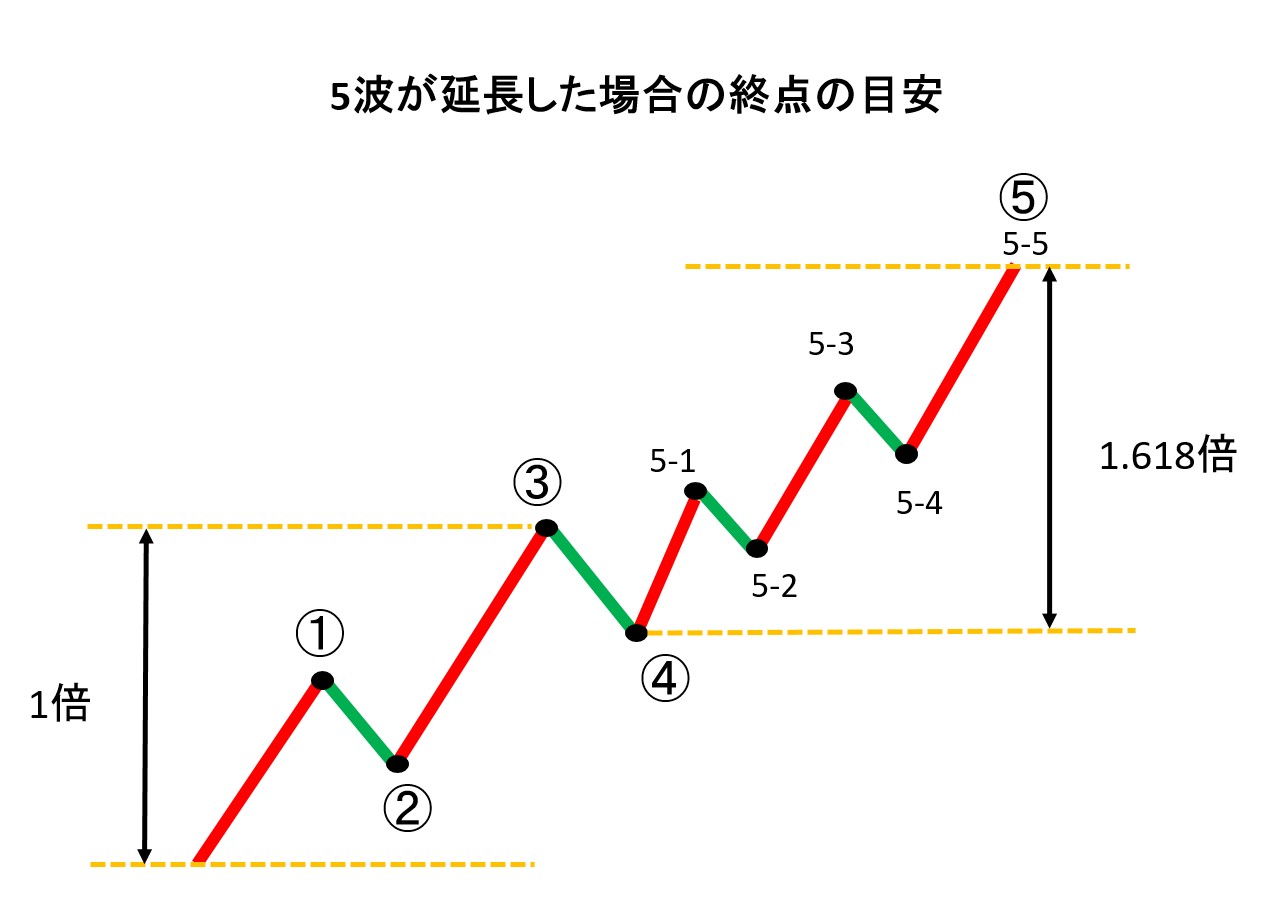
3-2. 延長(エクステンション)のないインパルスの比率関係
ここまで、1波、3波、5波のいわゆるアクション波が延長した場合の比率関係を説明してきた。
実は、延長した波を含まないインパルスは全体的な整合が取れており、4波でフィボナッチ比率の黄金比に該当する。下図参照
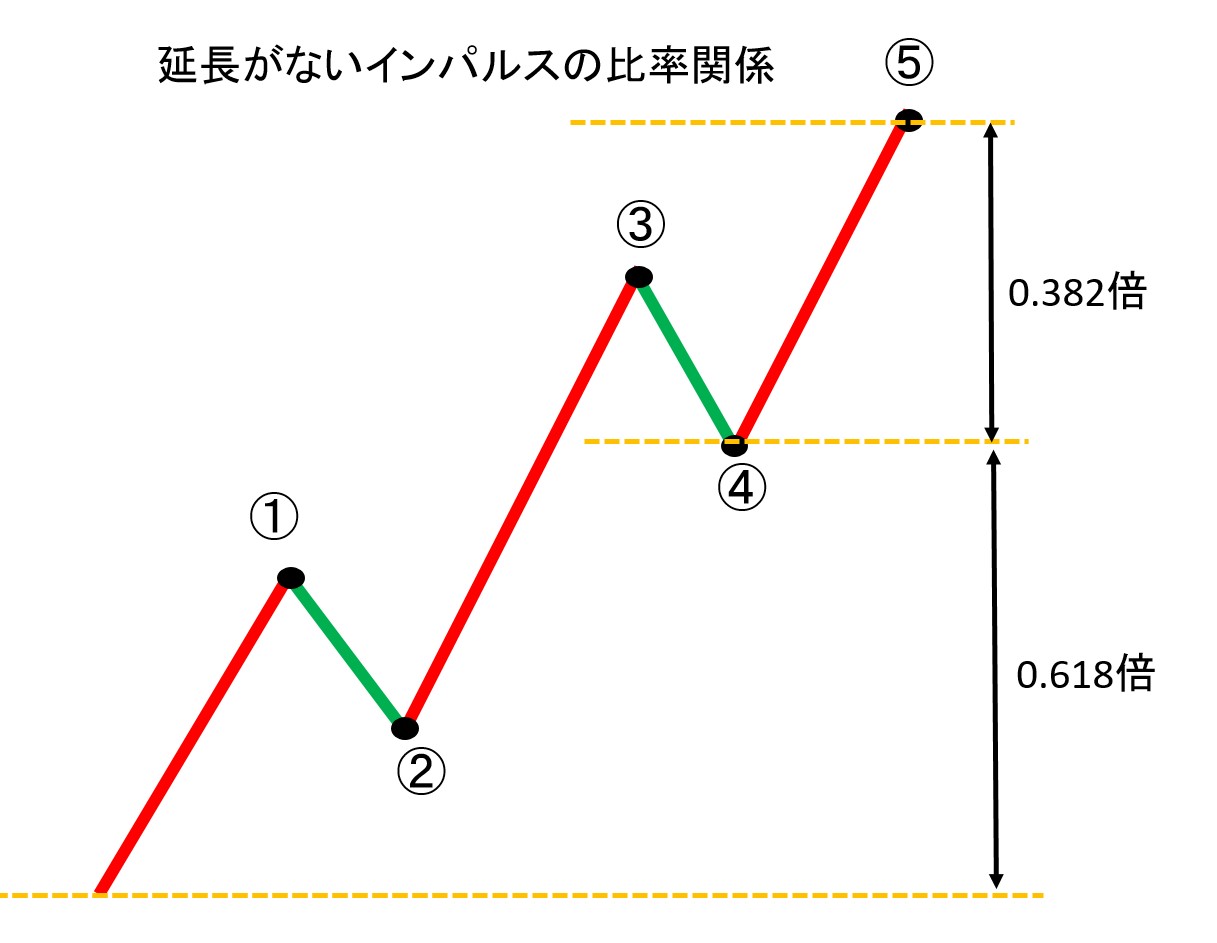
黄金比っていうのは、フィボナッチ比率の中で「0.382:0.618」、「1:1.618」のどちらかに当たる比率を意味する。これに加え、4波で分割できる箇所は黄金比を当てはめやすい。
ただ、実際のところは図のように完璧に4波の終点が分岐点になっているわけではない。むしろ、4波の始点から終点の範囲内が黄金比の分岐点になっていると知っておく必要がある。
3-3. 修正波内のアクション波の比率関係
ジグザグ、フラット・トライアングルの副次波にも、比率関係は存在する。繰り返しでくどいが、あくまでも目安ということで必ずその比率になるというわけではない。
しかし、知っていると相場の展開が自分のイメージ通りなのか?イメージと違った動きが始まったのか?ということが早い段階で察知できるようになる。
相場は生き物であり、必ずしも最初のイメージ通りに動くものではない。経験の浅い者は、最初のイメージに固執しすぎてしまい、イメージと違う展開になってもそれを認められず、ひどいことになりがちだ。
耳の痛い人も多いことだろう。
だが、比率関係を知ることで柔軟な対応が出来るようになり、トレードの成績も違ったものになってくるはずだ。難解であっても、めげないで読んでほしい。
3-4. ジグザグ・ダブルジグザグの比率関係
ジグザグのA波とC波の比率関係は、C波の大きさはA波と同じ大きさ、そうでない場合は0.618倍か1.618倍が目安になる。下図参照
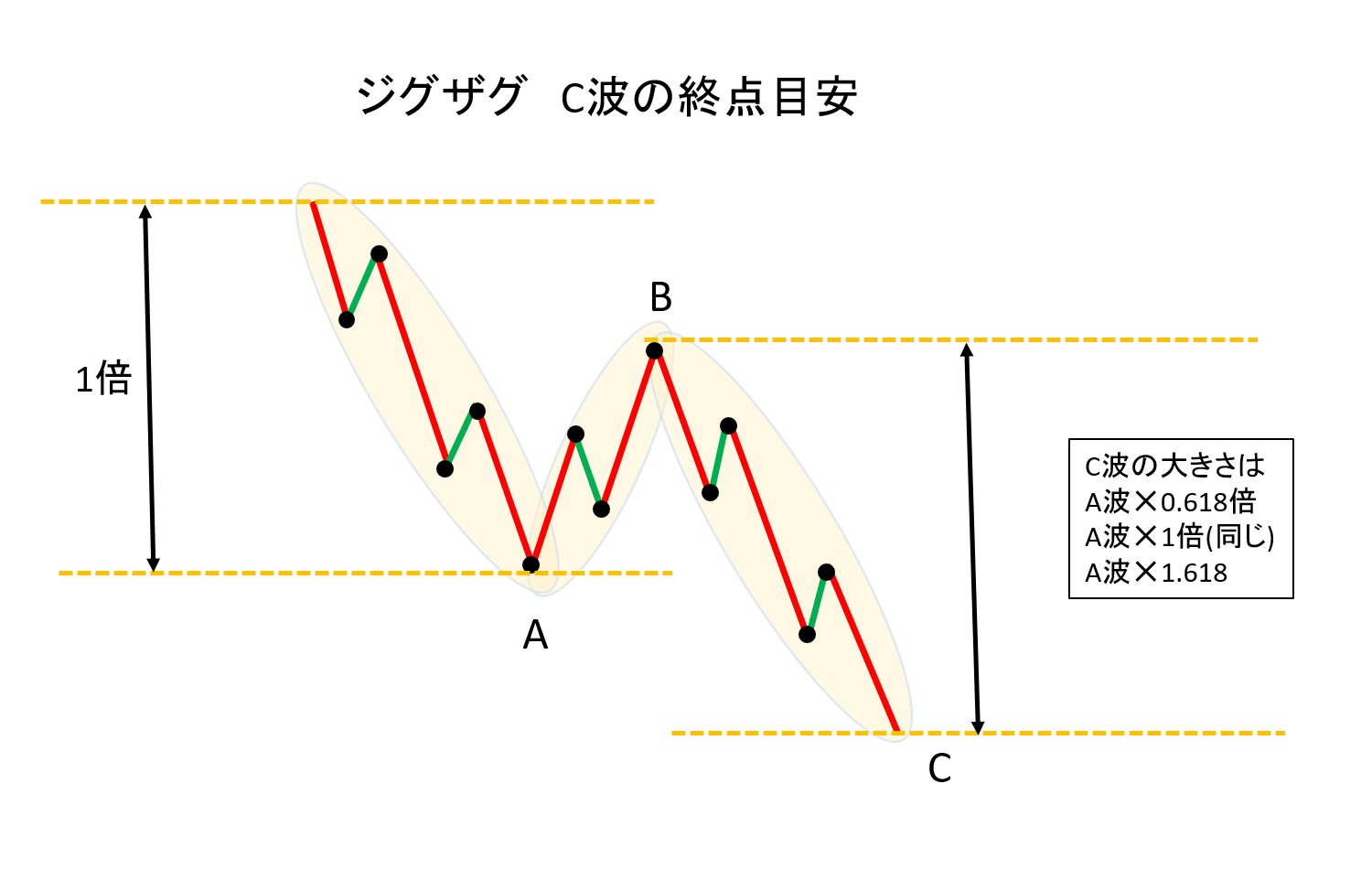
ダブルジグザグの場合は、最初のジグザグ(W波)と2つ目のジグザグ(Y波)も同様の比率になる。下図参照
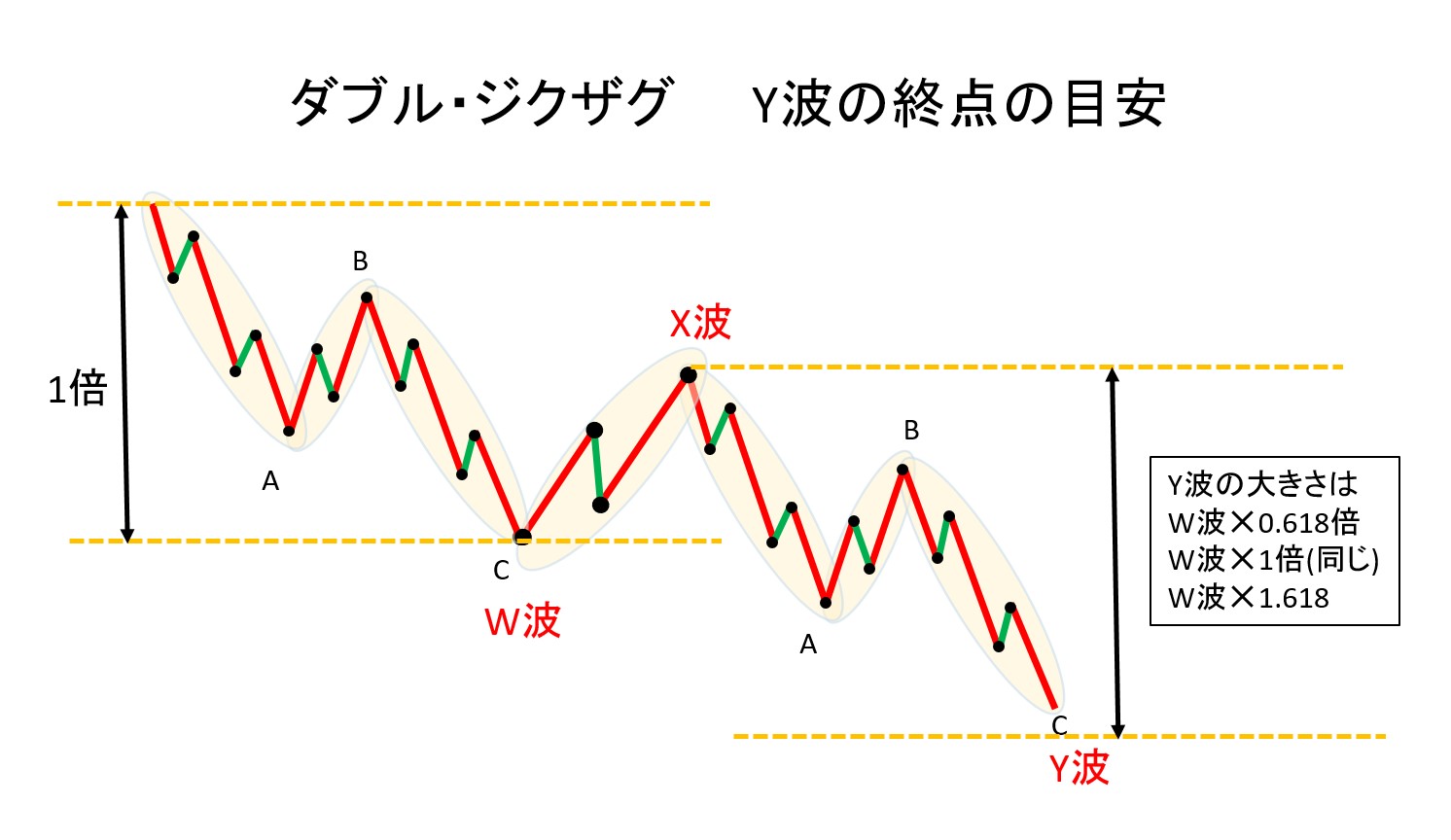
3-5. 拡大型フラットの比率関係
拡大型フラットのB波はA波の1.236倍や1.382倍がメドになる。早い話が、ザックリでA波の変化率の20%から30%飛び出すということだ。
例えばA波が10%であれば12%から13%といった感じだ。
相場では、フィボナッチの数字でピタって止まるわけではないので、このくらいアバウトに大体こんなもんだろうとイメージしておく。そして、そこで止まったら「あれ?どうしてかな?あーフィボだったのね」とこんな感覚でちょうど良い。
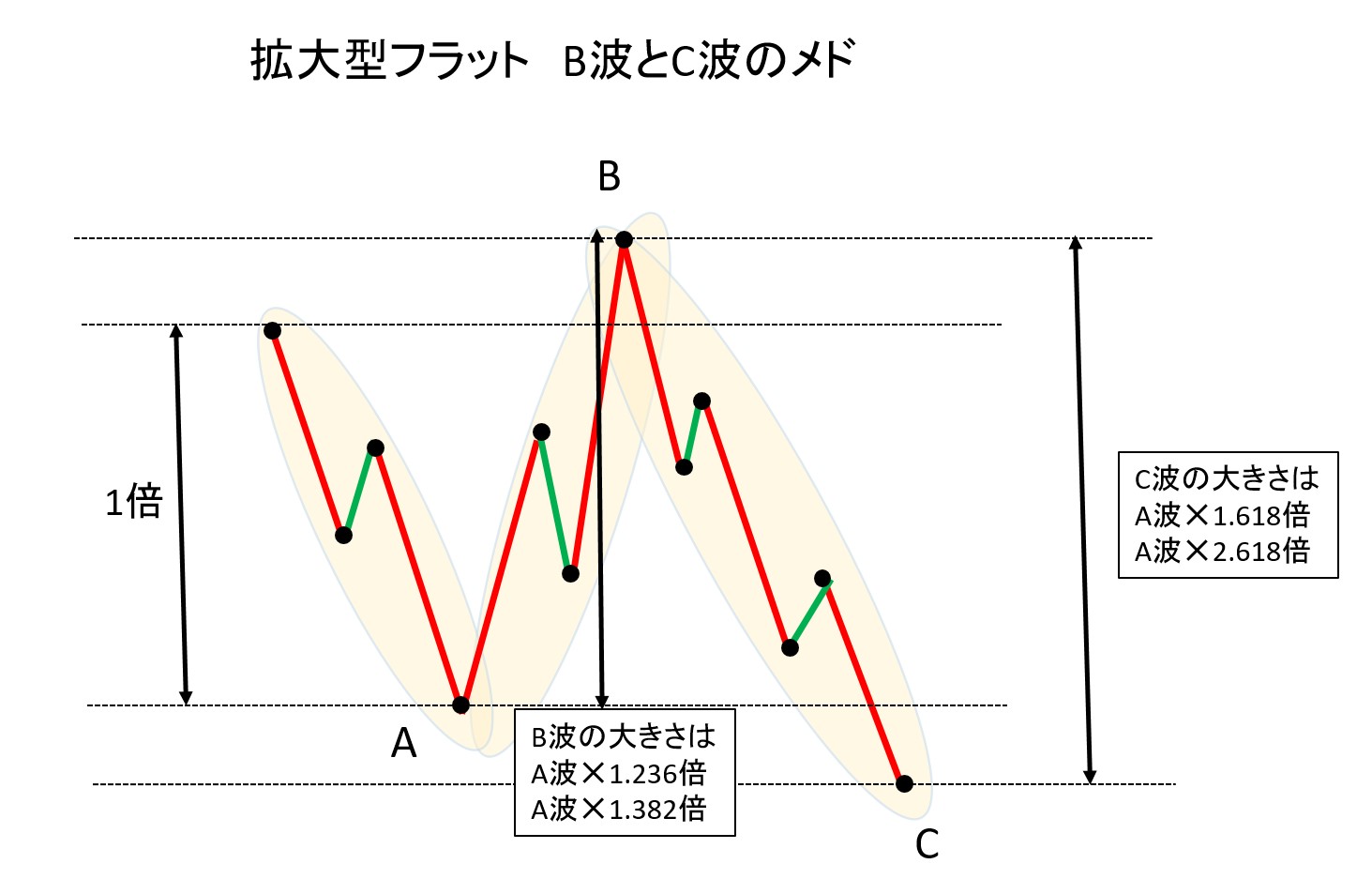
拡大型フラットのB波はA波の1.236倍や1.382倍がメドになる。そして、C波はA波の1.618倍か2.618倍が目安となる。
この測定の仕方は、チャートツールにあるフィボナッチ・エクスパンション(エクステンションも同義語)で簡単に測ることができる。(やり方はここでは割愛する。)
3-6. トライアングルの比率関係
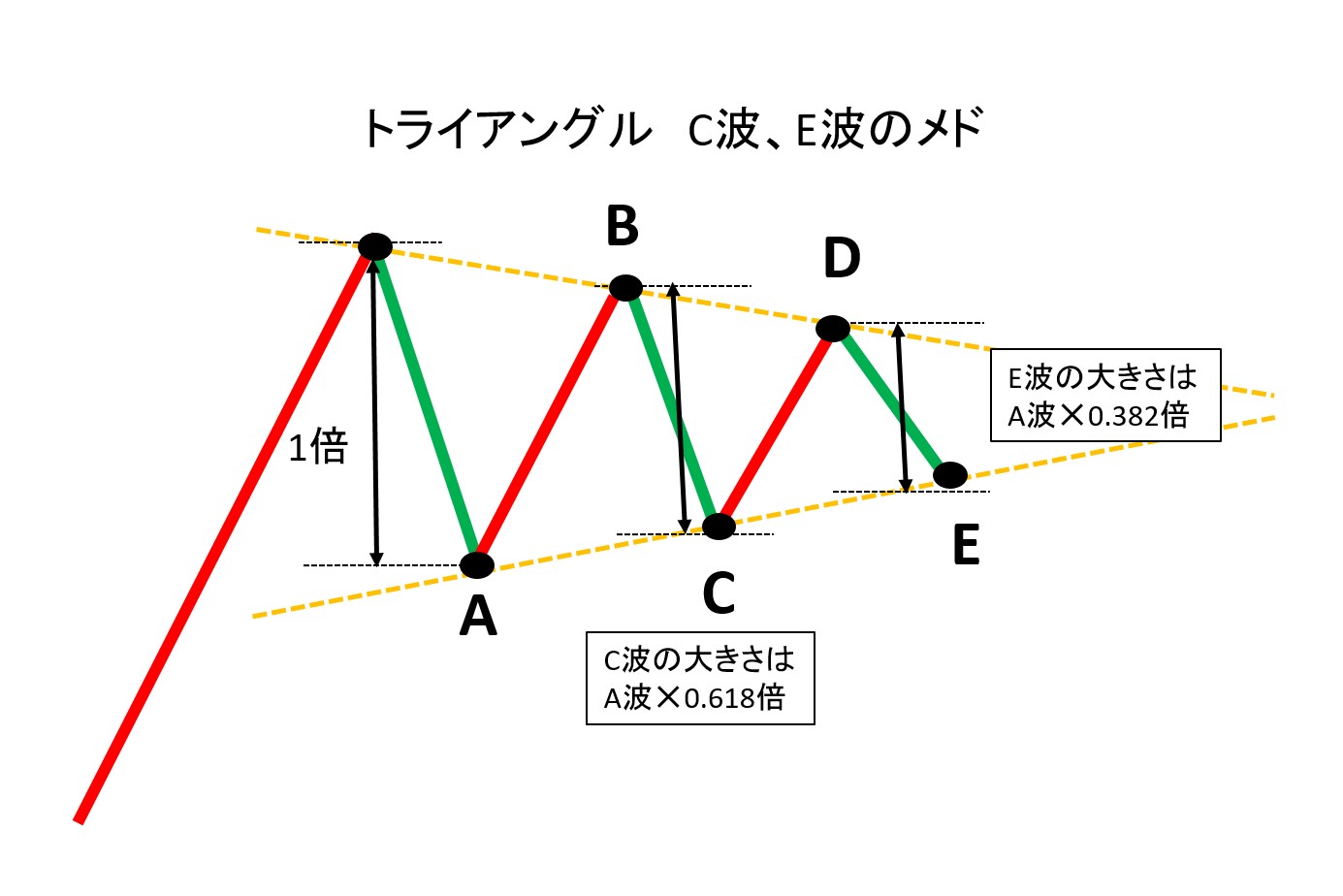
トライアングルの比率関係は、C波はA波の0.618倍、E波はA波の0.382倍(C波の0.618倍でも同じ。0.618✕0.618=0.382となる)が目安となる。
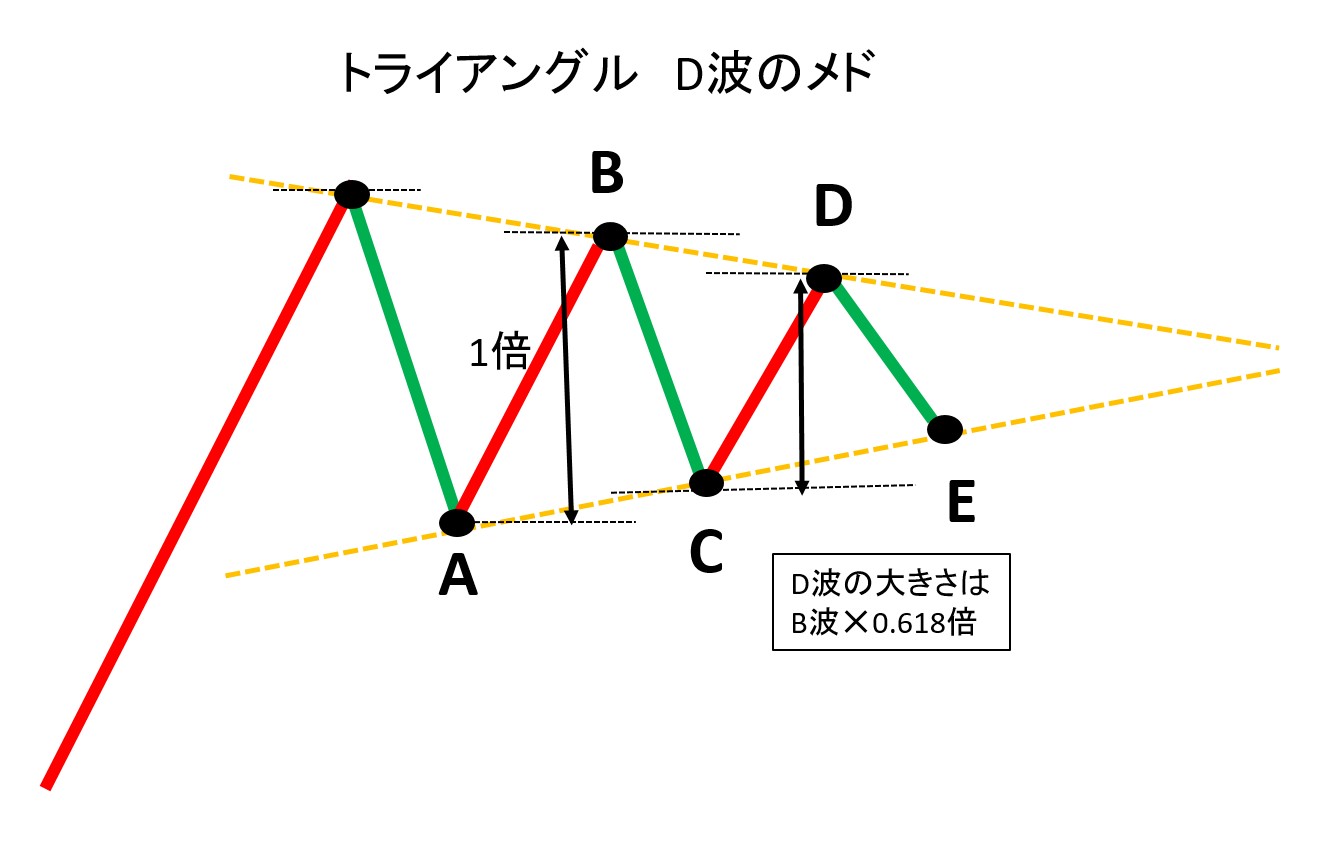
D波はB波の0.618倍が目安となる。拡大型の場合はこの比率が1.618倍となる。
これを知識として知っておくと、トライアングルを形成していることに早く気がつく。経験の浅い者は、A,B,C,D,Eと出来上がって飛び出してから気がついたりする。しかし、副次波同士の比率関係の目安を知っていると気がつくのに遅いということがなくなる。
また、拡大型の場合は後からになって拡大型と気がつくことが多いが、比率を知っているとある程度の段階で、もしかしたら拡大型かも?と察知することができる。
4. エリオット波動の比率関係まとめ

今回は、エリオット波動の比率関係について解説した。比率関係について知っておくと、波動終点のメドのおおよその見当を付けやすくなり、波動全体のバランスをチェックしやすくなる。
しかし、何度も言うが、フィボナッチの数字でキチっと止まったりするわけじゃない。おおよその目安でしかない。だがそれを複数イメージすることが出来ると、今まで気がつかなかった所でチャンスが見つかったりする。知っているのと知らないのとでは大きな差がつく。
次の記事は「修正波の深さ」について説明する。



 twitterを開く
twitterを開く Youtubeを開く
Youtubeを開く メルマガ登録する
メルマガ登録する