【具体例付き】ボリンジャーバンドの計算式って?原理を理解して使いこなす方法

ボリンジャーバンドは移動平均線と標準偏差で構成されており、よくトレンド分析に用いられます。
ボリンジャーバンドを利用するトレーダーの中には、「正確にテクニカル分析するために、仕組みを理解したい」と考える方もいるのではないでしょうか。
とはいえ理論や計算式を調べてみても、難しくて理解しにくいですよね。
そこで、当記事では画像を用いながらボリンジャーバンドの仕組みや計算式について解説します。
最後まで読めば、ボリンジャーバンドの指し示す情報を理解し、トレードの際に役立ちますよ!
目次
1. ボリンジャーバンドは移動平均線と標準偏差で構成される
ボリンジャーバンドは1本の移動平均線と、2本以上の標準偏差(σ)で構成されます。
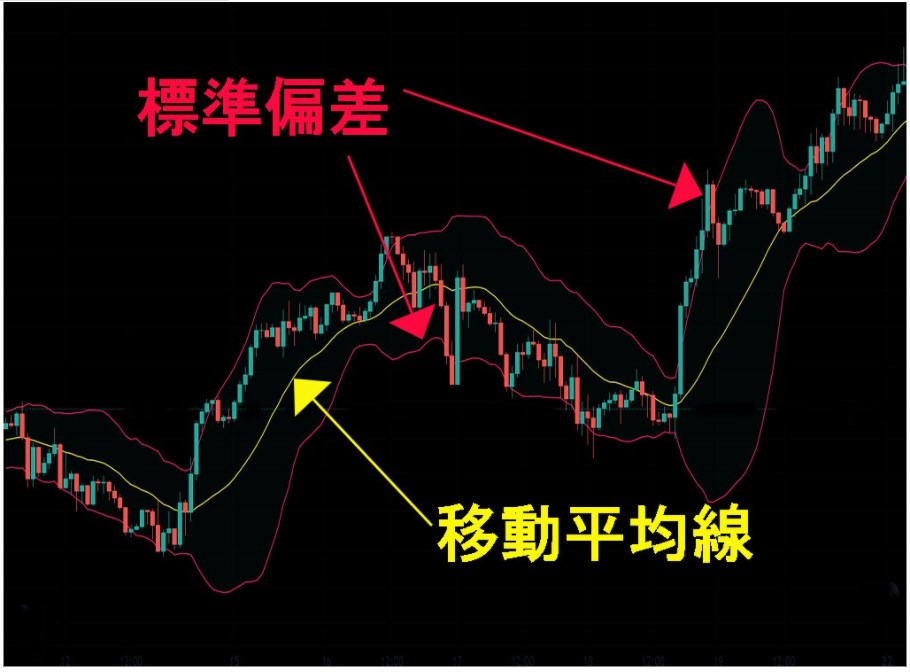
ローソク足上に1本の移動平均線、その上下に標準偏差が表示されます。
移動平均線が示す情報は、一定期間の終値の平均。
そして標準偏差は、平均価格との値幅を示します。
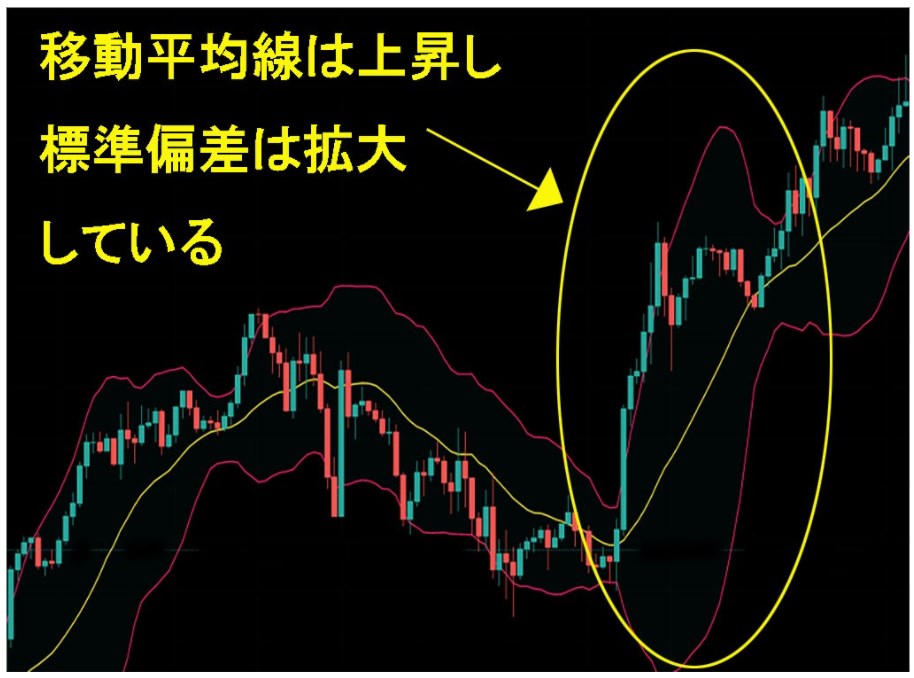
例えば上記のチャートをご覧ください。
こちらは期間を20日に設定したボリンジャーバンドです。
移動平均線は緩やかに上昇し、標準偏差は徐々に拡大しているのが分かりますね。
移動平均線が示すのは過去20日の終値の平均であるため、値上がりしていけば移動平均線も上がっていきます。
標準偏差が示すのは、過去20日間の平均価格との差。
標準偏差の拡大は、平均価格と大きな値幅を付けていることを意味します。
以上のようにボリンジャーバンドは、移動平均線と標準偏差がワンセットになっている指標です。
2. ボリンジャーバンドの計算式を解説!チャート上にはどう反映される?

ボリンジャーバンドは移動平均線と標準偏差で構成されていると解説しました。
実際、ボリンジャーバンドは下記の計算式で求められます。
ボリンジャーバンド=n日の移動平均 ± n日の標準偏差
ボリンジャーバンドは移動平均線の上下に標準偏差を表示させた指標。
そのため、移動平均線に標準偏差をプラス・マイナスすれば良いだけであると分かりますね。
それでは移動平均線と標準偏差は、どのような計算式で求められているのでしょうか。
ここでは移動平均線と標準偏差の計算式を、チャートを交えながら解説します。
2-1. 移動平均線の計算式
はじめに移動平均線の計算式をお伝えします。
移動平均線=過去n日分のローソク足終値の合計÷ n(日数)
この計算式は、平均を導く場合と同じです。
5個のリンゴの平均重量を計算する時は、全ての重さを足し、その合計値を5で割りますよね。
移動平均線も同様の方法で計算するのです。
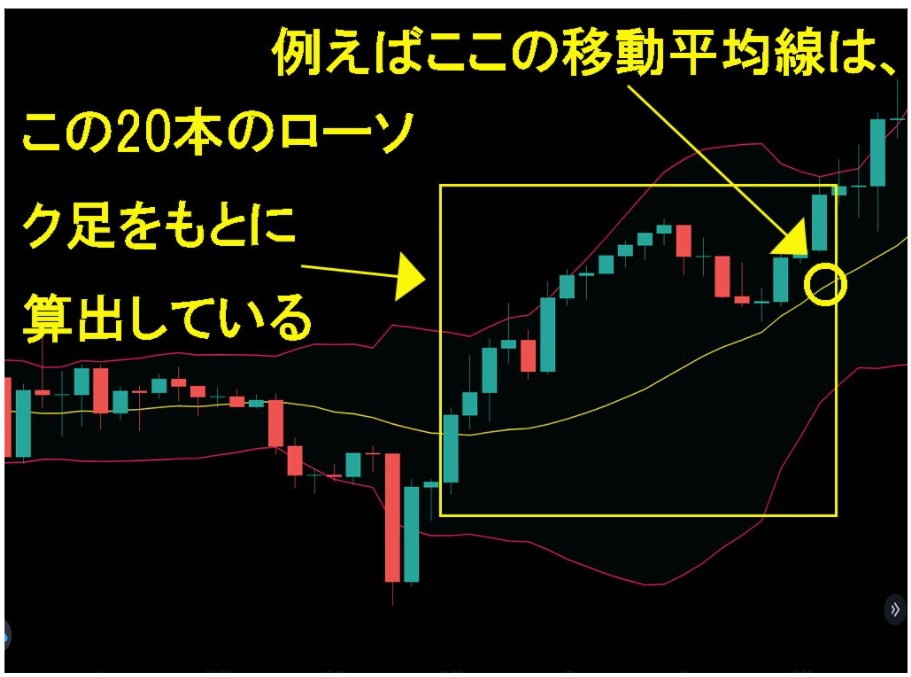
この画像は日足チャートであり、期間を20日に設定したボリンジャーバンドを表示しています。
真ん中の黄色い移動平均線も同様に20日。
画像内の黄色い矢印で指し示した移動平均線では、その時点から過去20日分のローソク足の終値を足し、合計値を20で割った数を示しているのです。
このチャートは日足チャートなので、20本分のローソク足の終値をもとに移動平均線が計算されています。
仮に設定期間を20日から50日に変え、日足チャートのままにした場合、移動平均線が指し示す情報はローソク足20本分ではなく50本分になります。
そしてチャートを日足から4時間足に変え、設定期間を20日のままにした場合、移動平均線が指し示す情報はローソク足120本分となるのです。
*20日=日足のローソク足20本分
24時間=4時間足のローソク足6本分
つまり、20日×4時間足6本(24時間)=4時間足120本。
このように移動平均線は、設定期間に応じたローソク足の終値の平均値を示すのです。
ローソク足と移動平均線を見れば、設定期間の平均より現在価格が高いか低いか判断できます。
2-2. 標準偏差の計算式
標準偏差の計算式は下記の通りです。
標準偏差=√(n×過去n日分のローソク足終値の2乗の合計-過去n日分のローソク足終値の合計の2乗)÷{n×(n-1)}
恐らく標準偏差の計算式を見てスムーズに理解するのは困難なので、計算式が何を意味しているのかだけ押さえてください。
標準偏差では、対象となるデータにどれほど数値のばらつきがあるかを計算します。
例えば、下記のような2つのデータがあったとしましょう。
- 対象① 80円・100円・120円
- 対象② 30円・50円・75円・100円・125円・150円・170円
対象①と②の平均価格を計算すると、ともに100円です。
しかし2つの対象データには、大きな値幅があると分かりますね。
対象①は最小価格80円、最大価格120円であり、値幅は40円です。
それに対して対象②は最小価格30円で、最大価格170円であり、値幅は140円。
つまり、対象①よりも対象②はデータの数値にばらつきが見られるのです。
この2つの対象を計算し、標準偏差で表した場合、対象②の方が大きな標準偏差になるでしょう。
なぜなら標準偏差は、データの数値のばらつきを示すためです。
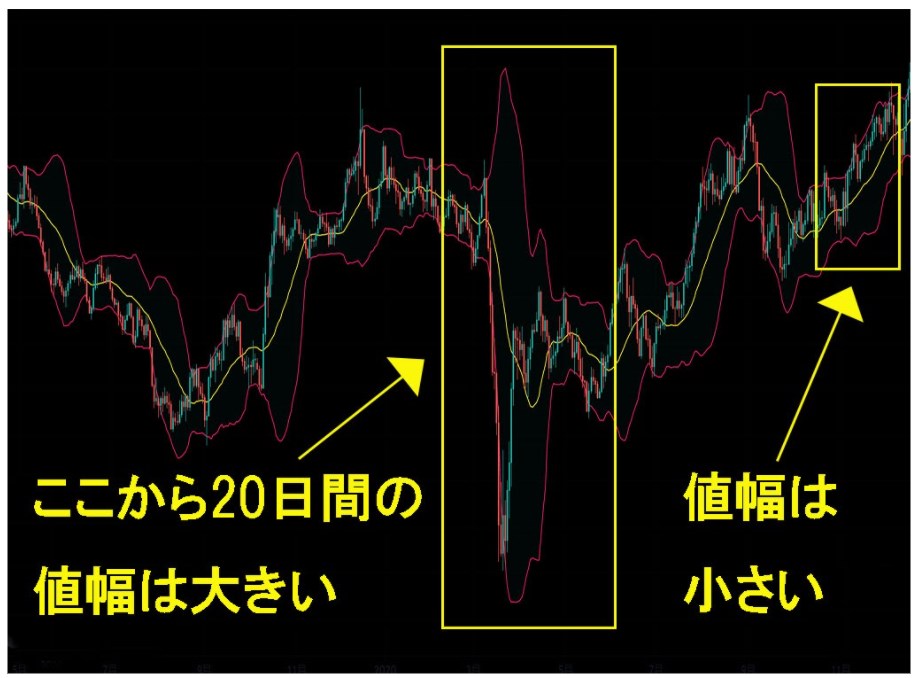
今度は実際のチャートで標準偏差について考えてみましょう。
日足チャート上に、期間20日のボリンジャーバンドを表示させました。
ボリンジャーバンドの標準偏差が示すのは、一定期間における通貨価格のばらつきになります。
すなわち、20日間の値幅の大きさを表しているのです。
チャート上では、ボリンジャーバンドの標準偏差が拡大しているところと、縮小しているところがありますね。
拡大しているところは、その時点から20日間における値幅が大きく、反対に縮小しているところは値幅が小さいと分かるのです。
もし20日間に大きく値動きしなければ、標準偏差は拡大しません。
一方で20日間で相場が急変すれば、値幅が広がり、標準偏差も拡大するでしょう。
このように標準偏差を利用すれば、どれほど対象データにばらつきがあるのか分かります。
実際のチャートを見て、移動平均線と標準偏差の計算をしようとしても、正確に計算するのは難しいと考えられますよね。
特に標準偏差は計算式自体が複雑です。
そのためボリンジャーバンドの計算をするのではなく、ボリンジャーバンドでどのような分析ができるのかを押さえましょう。
*ボリンジャーバンドを使用する際の期間設定については、「ボリンジャーバンドのおすすめ期間は?検証から分かる期間ごとの特徴を解説」にて詳しく解説しています。
3. ボリンジャーバンドの仕組みが分かれば売買サインを見つけられる

移動平均線は一定期間の平均価格を示し、標準偏差は一定期間の値幅の大きさを示すことを解説しました。
こうしたボリンジャーバンドの仕組みが分かれば、トレードに活用できます。
ボリンジャーバンドを利用した順張り・逆張り手法を解説しましょう。
尚、ボリンジャーバンドの詳しい見方についてはこちらの記事でも解説しているので、参考にしてみてくださいね。
3-1. 順張り手法の売買サイン
順張りをする場合、ボリンジャーバンドを利用してトレンドを見つける必要があります。
トレンドを見つける際に、移動平均線と標準偏差を活用するのです。
移動平均線は一定期間の価格平均を示すため、もし移動平均線が上がれば、上昇トレンドであると考えられるでしょう。
そして標準偏差は一定期間の値幅の広さを示すので、標準偏差の拡大は相場が変動し、トレンドの発生を予想できるのです。
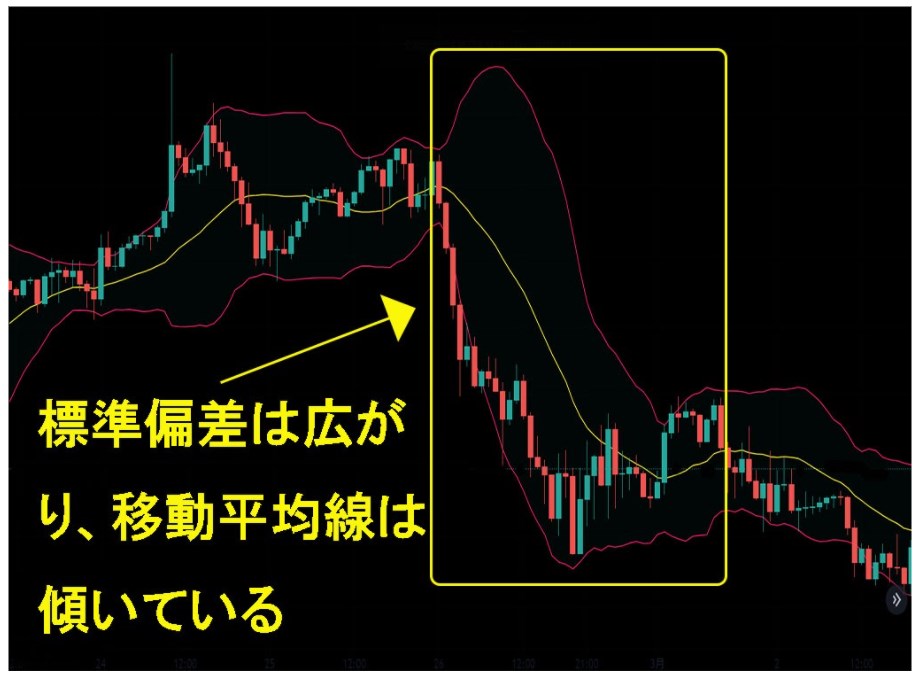
実際のチャートをご覧ください。
黄色の範囲では、標準偏差は広がり、移動平均線は下向きに傾いていますね。
設定期間中の平均価格は下落し、値幅が広がっていると分かるので、下降トレンドであると判断できるのです。
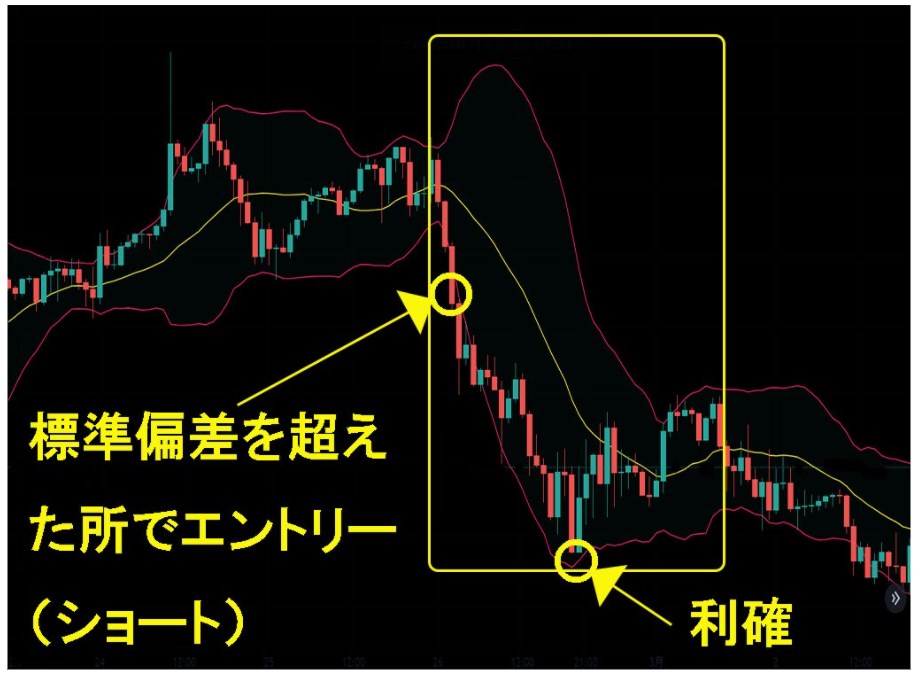
移動平均線の傾き・標準偏差の拡大を確認したら、ローソク足を見て売買ポイントを見つけましょう。
ボリンジャーバンドを活用した順張りでは、標準偏差を価格が超えたところをポイントとします。
それゆえに、価格が標準偏差を下抜けたところでショートエントリーしましょう。
利確ポイントの目安は、標準偏差の縮小を確認したところです。
標準偏差の縮小は一定期間の値幅が狭くなっていることを意味します。
値幅が狭くなれば相場の動きは小さくなっていると判断できるので、トレンド終了を予測できるのです。
したがって標準偏差が縮小したら、利確するのをおすすめします。
3-2. 逆張り手法の売買サイン
次は逆張り手法についてです。
逆張りする際はトレンド相場ではなく、レンジ相場を見つけます。
レンジ相場を見つける時は、移動平均線が並行に推移しているところと、標準偏差が縮小しているところを探しましょう。
移動平均線が一定の価格帯をキープしていれば、価格変動していないと判断できます。
加えて標準偏差が縮小していれば、値幅は狭いためトレンド相場ではないと分析できるのです。
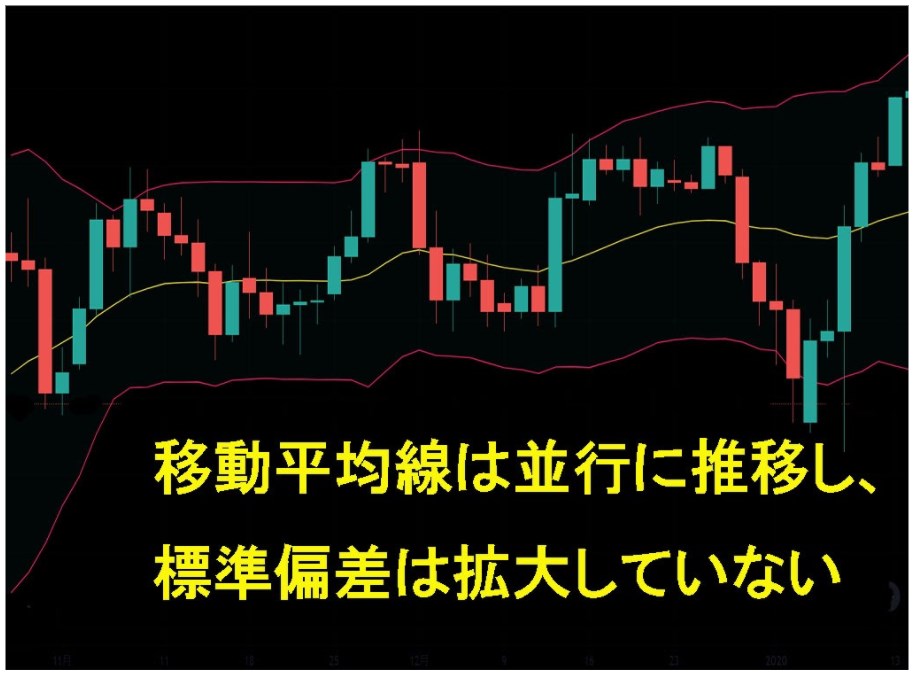
このチャートでは、移動平均線は一定の価格帯で推移しており、標準偏差は拡大していません。
レンジ相場であると分かるので、売買ポイントを見つけます。
ボリンジャーバンドを活用した逆張りでは、価格が標準偏差に達したところをエントリー・利確ポイントとします。
なぜならボリンジャーバンドでは、標準偏差の範囲内で値動きする確率が決まっているため。
標準偏差は1σ・2σ・3σの3種類に設定でき、それぞれの範囲で価格が推移する確率は下記の通り。
- ±1σの範囲内で推移する確率:約68.3%
- ±2σの範囲内で推移する確率:約95.4%
- ±3σの範囲内で推移する確率:約99.7%
画像のチャートは±2σに設定しているので、標準偏差の範囲を価格が超える確率は4.6%。
つまり、一時的に価格が標準偏差を超えても、高い確率で戻ると判断できるのです。
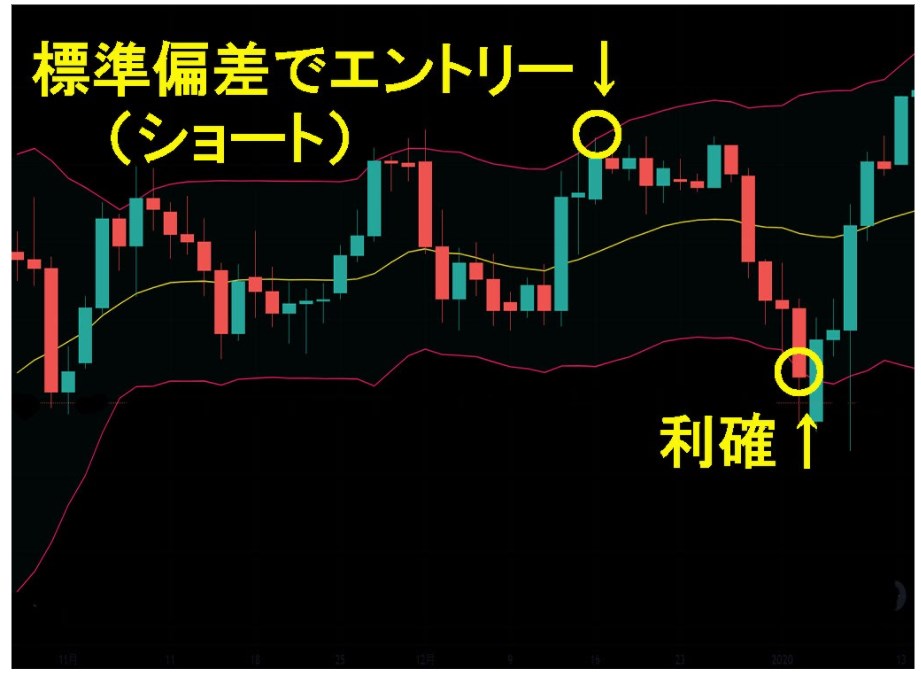
チャートでは、一時的に価格が標準偏差を上抜けしました。
売買ポイントに達したので、ここでショートポジションを持ちます。
レンジ相場では一定の範囲で値動きするため、もう一方の標準偏差に
価格が達したところで、利確しましょう。
4. まとめ

今回はボリンジャーバンドの計算式について解説しました。
ボリンジャーバンドは移動平均線と標準偏差で構成される指標。
移動平均線を求める計算式は理解しやすいですが、標準偏差の計算式は複雑です。
とはいえ、計算式を理解して実際に計算できるようになる必要はありません。
テクニカル分析の目的は、相場認識をしてトレードで勝つこと。
そのためボリンジャーバンドでどのような分析が可能かを押さえましょう。
この記事を参考にして、ボリンジャーバンドが示す情報の意味を理解し、トレードに役立ててください。
サンプルの文字
サンプルの文字2



 twitterを開く
twitterを開く Youtubeを開く
Youtubeを開く メルマガ登録する
メルマガ登録する




